1086-1093年，宋朝的沈括在《梦溪笔谈》中提出“隙积术”和“会圆术”，前者是高阶等差数列求和法，后者是关于弓形的计算。

隙积术指如何计算垛积，沈括运用类比、归纳的方法，以体积公式为基础，把求解不连续个体的累积数，化为连续整体数值来求解，已具有了用连续模型解决离散问题的思想。在中国数学史上，发展了自南北朝时期就停滞不前的等差级数求和问题，并推进到高阶等差级数求和的新阶段，开创了中国垛积术研究的先河。

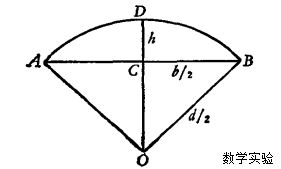
会圆术，实际上是指由弦求弧的方法，其主要思路是局部以直代曲，对圆的弧矢关系给出一个比较实用的近似公式。在中国数学史上，沈括第一个利用弦、矢求出了孤长的近似值。这一方法的创立，不仅促进了平面几何的发展，而且在天文计算中也起了重要的作用，为中国球面三角学的发展作出了重要贡献。